| Author: |
Jan Heller, homepage, <hellej1 AT cmp.felk.cvut.cz> |
| Advisor: |
Ing. Tomas Pajda, Ph.D., homepage, <pajdla AT cmp.felk.cvut.cz> |
| Affiliation: |
Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University in Prague |
| Defence: | April 13, 2016 |
Abstract
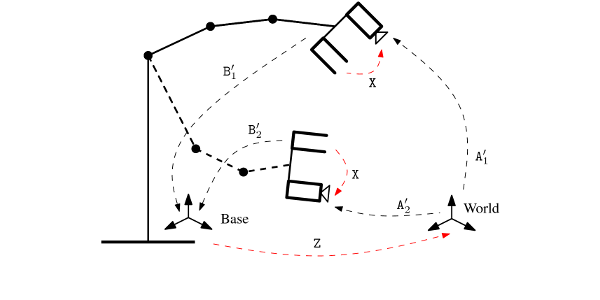
The need to relate measurements made by a camera to a different known coordinate system arises in many engineering applications. Historically, it appeared for the first time in the connection with cameras mounted on robotic systems. This problem is commonly known as hand-eye calibration. In this thesis, we study the problem of hand-eye calibration as well as a problem closely connected to it---the problem of robot-world calibration. The first objective of this work is to apply recent results in mathematical optimization to provide globally optimal solution to these problems. The second objective is to formulate and study these problems as minimization problems under some geometrically meaningful error measures using image measurements directly. We also study global optimizers in situation where image measurements are not available using the classical problem formulations. The solutions presented in this thesis are compared to existing methods and validated by both synthetic and real world data experiments.
In the first part of the thesis, we survey the state of the art of the camera-robot calibration as well as of the main concepts of the geometrical computer vision. Further, we review several results in the globally optimization techniques and their application in the computer vision.
Next, we formulate the problem of hand-eye calibration as a minimization problem under some geometrically meaningful error measures. We provide two solutions; the first solution employs a Structure-from-Motion approach and the Second Order Cone Programming optimization and the second one uses the Brand-and-Bound optimization strategy. Both solutions provide globally optimal minimizers and work with image measurements directly, instead of using them as a pre-step for explicitly calculating camera poses. Using a similar approach, we also formulate a minimization task for the robot-world calibration problem. This time, to solve the task we use the method of Linear Matrix Inequality relaxations.
Further, we investigate the problem of hand-eye calibration in situations, where the information about the rotation of the robot is not known. This problem arises when the robot is not calibrated or the information from the robot is not available. We use the method of Gröbner basis to deal with this scenario.
Finally, we revisit the classical formulation of the hand-eye and robot-world calibration. Using the method of Linear Matrix Inequality relaxations, we provide several global optimizers in situations, where image measurements are not available and the calibration has to be estimated from robot and camera poses only.