Algorithms and Data Structures for Very Large Sparse Matrices

Summary

Title: Algorithms and Data Structures for Very Large Sparse Matrices
Author: Ing. Daniel Langr, Ph.D.
Supervisor: prof. Ing. Pavel Tvrdík, CSc.
Defense: May 22, 2015
Organization: Faculty of Information Technology, Czech Technical University in Prague

Downloads

Abstract

Sparse matrix-vector multiplication (SpMV) is one of the most important numerical core methods in scientific and engineering computing. On today's petascale and future exascale systems, the three principal problems related to SpMV are the minimization of communication between processors in distributed-memory environments, the maximization of the efficiency of local SpMV performed by a single processor, and the implementation of efficient resiliency to system failures by either checkpointing-restart (C/R) or C/R-free techniques. A general solution of these problems is far beyond the scope of a single scientific work. This thesis deals with several research tasks related to large-scale SpMV-based computations, which include the design of a space-efficient storage format for sparse matrices and development of accompanying algorithms, the experimental evaluation of suitability of this format for storing matrices to parallel file systems, the definition of generic criteria for evaluation of sparse storage formats, the design of parallel scalable generator of benchmark sparse matrices, the development of downsampling and visualization algorithms for large sparse matrices, and the implementation of fast parallel generator of large-scale random permutations.

Awards

This work was awarded 2nd place in 2014 Joseph Fourier Prize in Computer Science. [Diploma]

Selected Relevant Publications

  • D. Langr, P. Tvrdík. Evaluation Criteria for Sparse Matrix Storage Formats. IEEE Transactions on Parallel and Distributed Systems, 27(2):428–440, 2016. [DOI]

  • D. Langr, P. Tvrdík, I. Šimeček, T. Dytrych. Downsampling Algorithms for Large Sparse Matrices. International Journal of Parallel Programming, 43(5):679–702, 2015. [DOI]

  • D. Langr, P. Tvrdík, T. Dytrych, J.P. Draayer. Algorithm 947: Paraperm: Parallel Generation of Random Permutations with MPI. ACM Transactions on Mathematical Software, 41(3):5:1–5:24, 2014. [DOI]

  • D. Langr, I. Šimeček, P. Tvrdík, T. Dytrych. Large-Scale Visualization of Sparse Matrices. Scalable Computing: Practice and Experience, 15(1):21–31, 2014. [DOI]

  • D. Langr, I. Šimeček, P. Tvrdík, T. Dytrych. Scalable Parallel Generation of Very Large Sparse Benchmark Matrices. In Proceedings of the 10th International Conference on Parallel Processing and Applied Mathematics (PPAM 2013). Lecture Notes in Computer Science, 8384:178–187, 2014. [DOI]

  • D. Langr, I. Šimeček, P. Tvrdík, T. Dytrych, J.P. Draayer. Adaptive-Blocking Hierarchical Storage Format for Sparse Matrices. In Proceedings of the Federated Conference on Computer Science and Information Systems (FedCSIS 2012), 545–551, 2012. [HTTP]

Images

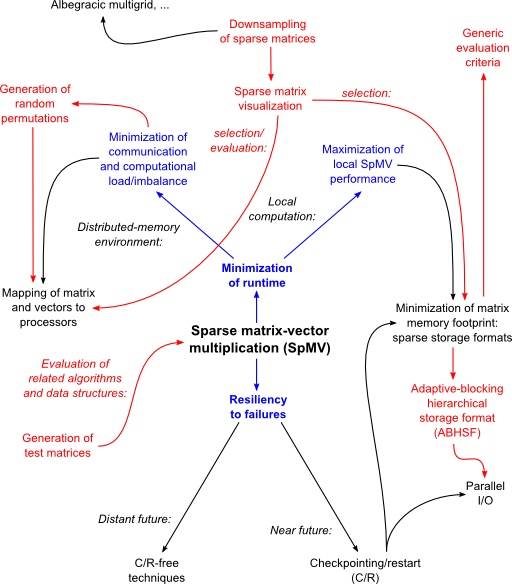
Contributions of the thesis (red) in the context of today's and future problems related to large-scale sparse matrix-vector multiplication (blue):

Contributions of the Thesis

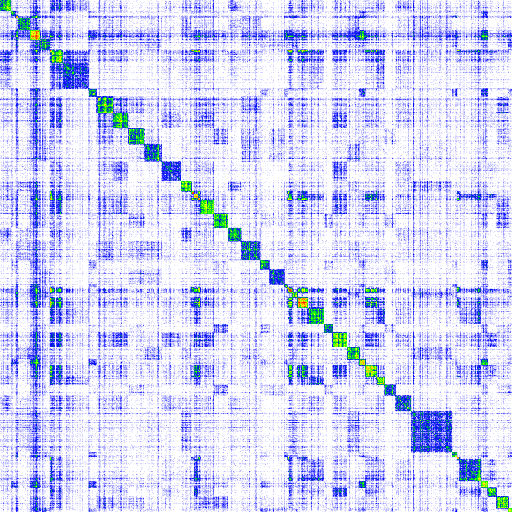
Visualization of the density of nonzero elements of a large sparse matrix:

Matrix visualization

Contact

Daniel Langr

e-mail: daniel.langr(at)fit.cvut.cz

Department of Computer Systems

Faculty of Information Technology

Czech Technical University in Prague

Menu