

A rank-decomposition of C5 (on the left) and a labeling parse tree of the same graph (on the right).
The subject of the thesis is the study of the parameterized complexity approach in developing graph algorithms. The approach allows the use of so-called parameters to obtain efficient graph algorithms on a very wide class of graphs. The thesis provides algorithms for a range of graph problems, gives hardness results and proves various structural and algorithmic properties of graphs.
Most of the thesis focuses on a relatively new structural parameter called rank-width. It shows that rank-width is a very powerful tool for dealing with a large number of interesting problems on graphs, including the design of efficient parameterized algorithms for many interesting problems on the large class of graphs of bounded rank-width. The thesis also provides an overview of various previously considered parameters on directed graphs and compares these to a directed version of rank-width with respect to how useful these parameters are in the design of parameterized algorithms. Interestingly, the results of this comparison are heavily in favor of the introduced directed version of rank-width.
Furthermore, the thesis contains a range of supplementary results. These include an analysis of the parameterized complexity of the well-studied Max-Rep and Min-Rep problems with respect to various parameters, and the introduction of twin-cover, a generalization of vertex cover which may be used as a powerful graph parameter capable of solving many notoriously hard problems.
The design of graph algorithms has become a focal point of computer science research in the past decades for practical as well as theoretical reasons. Graphs have turned out to be perfect models for an immense range of systems, both in practical settings and theoretical research. Unfortunately, most interesting problems on graphs do not seem to admit simple polynomial algorithms. Parameterized complexity is a rapidly developing, young and fresh field in theoretical computer science which provides the tools needed to deal with this fundamental problem. Many new results are discovered and published in the best scientific conferences each year, and the list of the practical applications of various parameters is growing rapidly.
The idea behind parameterized complexity lies in the fact that while most interesting problems are hard in general, in practice it is often not necessary to solve these problems on truly general instances. The input graphs of real-life algorithms are the outputs of other processes, such as natural selection, chemical and physical processes, and other algorithms. While these input graphs may be very large and complex, some structure is almost always present. The general idea of the parameterized algorithmic approach lies in exploiting this structure to obtain efficient algorithms.
To explain the concept of parameterized complexity, let us consider the well-known VERTEX COVER graph problem. A vertex cover
of a graph is a set of vertices such that every edge is incident to at least one vertex in the vertex cover.
Then we define the following problem:
INSTANCE: A graph G and a number k.
QUESTION: Does G have a vertex cover of size k?
This is known to be an NP-hard problem by standard complexity analysis, and so we cannot hope for a polynomial algorithm. However, we may use parameterized complexity to provide a more in-depth analysis of the complexity of this problem. To do so, we define a parameter, which is a function from the input to (usually) natural numbers, and search for algorithms which "blame" the overall complexity of the problem only on the parameter. In our case, k would be a natural choice for the parameter, and this allows us to propose the following two algorithms:
The thesis focuses on the field of parameterized complexity and provides a range of important results in three particular areas of interest:
Tree-width has proven to be a very successful parameter, with a range of applications in theory and practice. In the past decade, a significant amount of effort has been made to generalize the positive algorithmic results obtained on tree-width to a more general parameter, specifically a parameter which would attain low values even on complete graphs. This has lead to the introduction of clique-width.
Despite the initial success of clique-width, and particularly the extension of Courcelle's theorem to clique-width, the parameter suffered from one significant problem. Parameterized algorithms for tree-width and clique-width alike require so-called "decompositions" to work. In the case of tree-width, we speak of tree-decompositions, and these may be obtained by an FPT algorithm on graphs of bounded tree-width. On the other hand, there is no known FPT algorithm which would find optimal clique-decompositions (often called k-expressions) on graphs of bounded clique-width. In practice, this means that the vast majority of FPT algorithms parameterized by clique-width either assume that a k-expression is conveniently provided by an oracle, or use k-expressions obtained by approximation algorithms with an exponential error.
Rank-width was introduced as an alternative to clique-width, which had the distinct advantage that there exists an efficient FPT algorithm to compute optimal rank-decompositions. Since the rank-width of a graph is bounded if and only if its clique-width is bounded, designing FPT algorithms parameterized by rank-width would avoid the problems associated with clique-width while retaining efficient running times on the same wide range of graph classes.
This part of the thesis introduces a general framework which allows the design of efficient FPT algorithms on graphs of bounded rank-width. Unlike clique-width or tree-width, the original definitions of rank-width and rank-decompositions are not suitable for the direct design of parameterized algorithms. The thesis introduces so-called labeling parse trees, and show that these allow the design of parameterized algorithms which are exponentially faster than the best previously known alternatives on clique-width.


The results of this part include:
Following the success of tree-width, a number of different parameters for directed graphs were introduced with the goal of finding a suitable directed counterpart to tree-width. Parameters such as Directed Tree-width, DAG-width, D-width, Kelly-width were introduced and studied, and while they each differed from the others in the details of their definitions, they all shared several similarities and were based on the same design principles. Most notably, they all attain low (constant) values on directed acyclic graphs (DAGs).
This part contains an in-depth study of these "traditional" measures/parameters of directed graphs and a comparison of these measures to bi-rank-width, which is a generalization of rank-width to directed graphs. The complexity results indicate that while bi-rank-width retains its ability to solve a wide range of different problems on directed graphs, traditional measures are only suitable for the design of efficient algorithms for a few isolated problems. Additionally, this fact holds even if we significantly restrict the traditional measures by additional (natural) constraints. The obtained results are summarized in the following table:
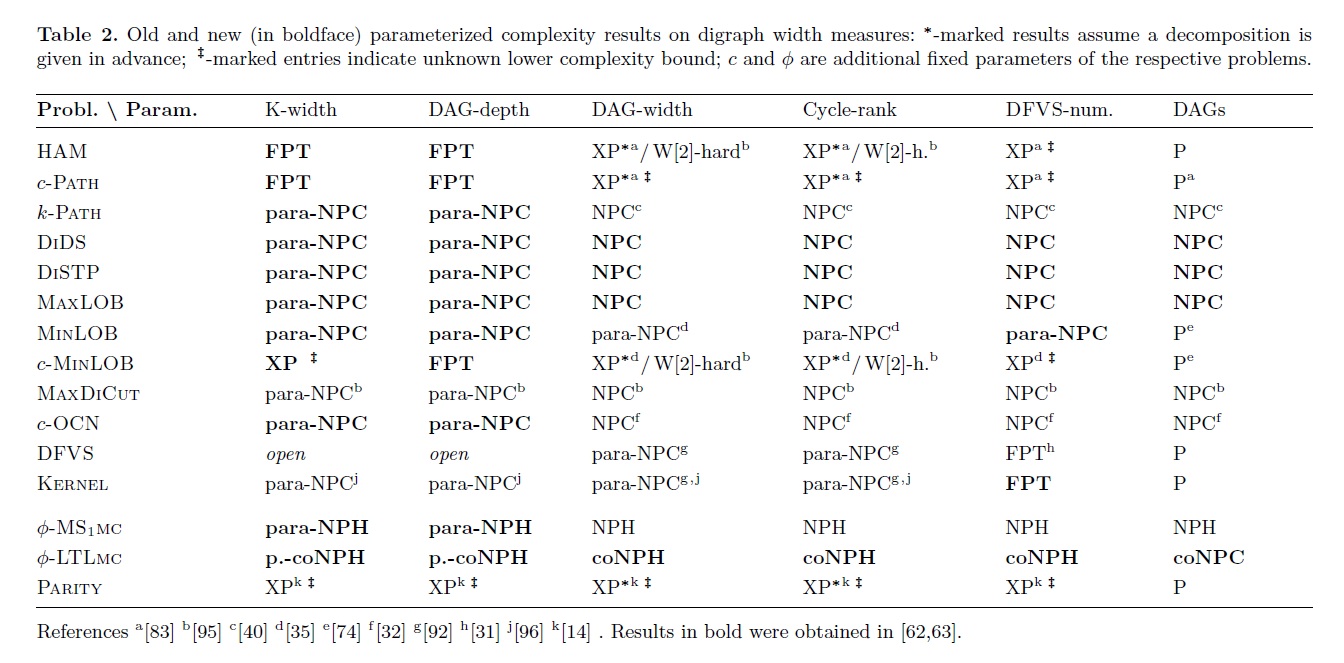
The thesis concludes this part by a general theorem, which says that any directed graph parameter with the same general properties as those which are fundamentally present in "traditional" digraph measures cannot admit efficient parameterized algorithms for MS1 model checking (i.e. some problems defined in the MS1 framework remain NP-hard). On the other hand, there is an FPT algorithm for MS1 model checking parameterized by bi-rank-width.
The final part of the thesis contains results on the design of efficient parameterized algorithms with non-standard parameters. The first section deals with the well-studied Max-Rep and Min-Rep problems, which have a long list of applications in other fields of computer science. The thesis provides an in-depth study of the parameterized complexity of these two problems, with several negative and positive results for various parameters.
The second section focuses on twin-cover, which is a generalized version of vertex cover. Vertex cover, aside from being a well-known graph problem, has historically also been used as a parameter for solving a multitude of various difficult problems. Specifically, recent advances in bioinformatics as well as other fields have lead to the introduction of many practically motivated problems which are not approximable and do not admit FPT algorithms even when parameterized by tree-width. It turns out that the vast majority of these problems still admit FPT algorithms when parameterized by the size of the minimum vertex cover.
However, the use of vertex cover is severely limited by the fact that it is too "restrictive" - very few graphs of interest have a sufficiently low vertex cover number. Twin-cover significantly improves on this aspect: the size of a minimum twin-cover is always smaller or equal to the minimum vertex cover, and may be significantly (arbitrarily) smaller than the vertex cover on some graph classes. On the other hand, almost all problems which are in FPT when parameterized by vertex cover are also in FPT when parameterized by twin-cover, and the runtime cost of using the more general twin-cover is usually negligible.
The final section of the thesis introduces a few results and parameterized algorithms on linear rank-width. Linear rank-width is a restriction of rank-width which is in many ways analogous to the way path-width is a restriction of tree-width. While linear rank-width has the potential to allow the design of efficient parameterized algorithms even for problems which are NP-hard on graphs of bounded rank-width (and even tree-width), new algorithmic methods will likely be required to obtain such algorithms. The thesis makes the first steps in this direction by providing a characterization of graphs of linear rank-width 1 as well as several polynomial algorithms on graphs of linear rank-width 1.
